Las funciones son una de las piedras angulares de las matemáticas, pero ¿qué son realmente? Imagina que una función es como una máquina mágica. Metes un número (o un conjunto de números) y, tras un proceso, sale otro número. Pero, ¿cuáles son los componentes de esta máquina? En este artículo, vamos a desmenuzar lo que es una función, sus elementos esenciales y cómo podemos utilizarlas en nuestra vida diaria. No te preocupes, no necesitas ser un experto en matemáticas para entenderlo. Vamos a hacerlo simple y divertido.
¿Qué es una función?
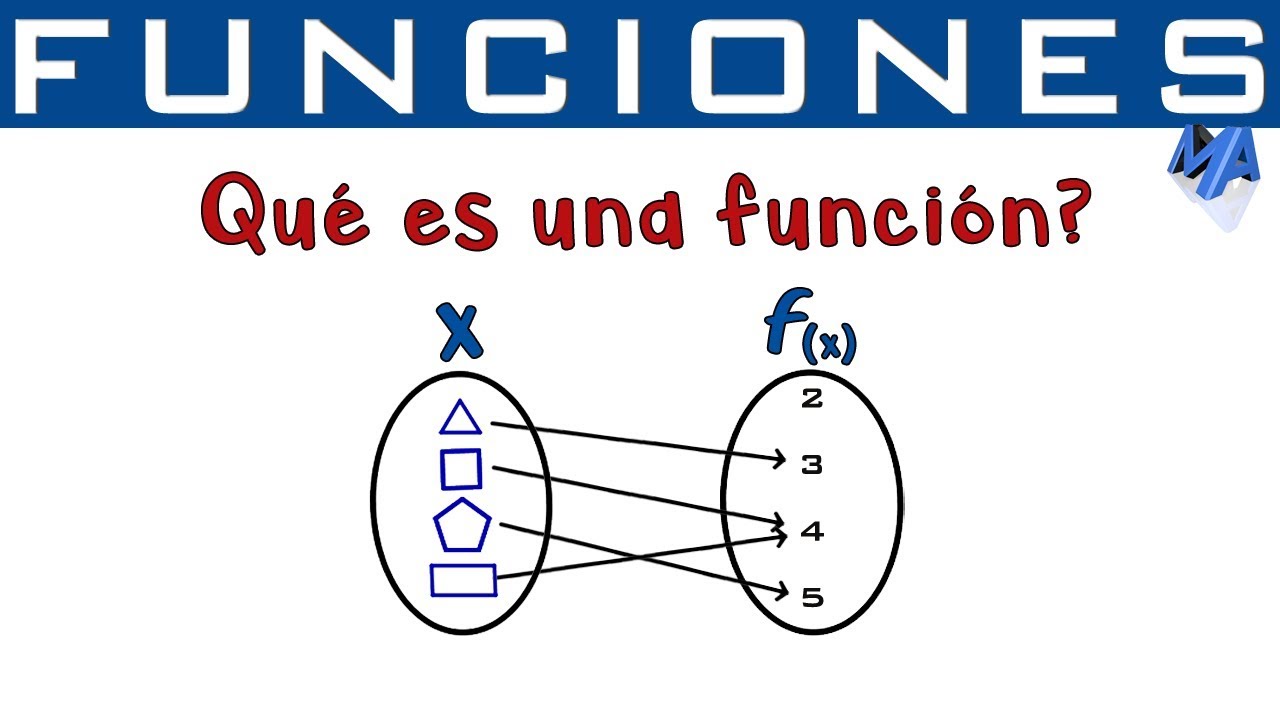
Una función es una relación matemática que asigna a cada elemento de un conjunto (llamado dominio) exactamente un elemento de otro conjunto (llamado codominio). En otras palabras, para cada entrada hay una única salida. Puedes pensar en esto como un restaurante: si pides una pizza, no puedes recibir una hamburguesa al mismo tiempo. Esto es lo que hace una función: establece reglas claras sobre cómo se relacionan las entradas y las salidas.
Ejemplo básico de una función
Imagina que tienes una función simple que suma 2 a cualquier número que le des. Si le das 3, la salida será 5. Si le das 7, la salida será 9. Cada número que ingresas tiene una única salida, lo que significa que esta relación es una función. Este concepto puede parecer un poco abstracto al principio, pero a medida que profundizamos, verás que las funciones están en todas partes.
Elementos de una función
Ahora que sabemos qué es una función, es hora de desglosar sus elementos fundamentales. Las funciones no son solo números; tienen componentes que son cruciales para su definición. Vamos a explorarlos uno por uno.
Dominio
El dominio de una función es el conjunto de todas las posibles entradas. Regresando a nuestra analogía del restaurante, el dominio sería el menú. Son las opciones que puedes elegir. Por ejemplo, si tienes una función que toma números del 1 al 10, esos son los únicos números que puedes usar. Si intentas ingresar 11, la máquina simplemente no sabe qué hacer.
Codominio
El codominio es el conjunto de todas las posibles salidas de una función. Siguiendo con nuestra analogía, si el menú del restaurante ofrece solo pizzas y pastas, entonces el codominio está limitado a esos platillos. En términos matemáticos, el codominio puede ser más amplio que el rango, que es el conjunto real de salidas que obtienes al aplicar la función.
Regla de correspondencia
La regla de correspondencia es lo que define cómo se relacionan las entradas y salidas. Es como la receta de un platillo: establece cómo se combina cada ingrediente para obtener un resultado delicioso. En matemáticas, esta regla puede ser una ecuación, como f(x) = x + 2. Aquí, estás diciendo que para cualquier x que ingreses, simplemente le sumas 2 para obtener el resultado.
Tipos de funciones
Las funciones no son un grupo homogéneo; hay muchos tipos diferentes, cada uno con sus propias características y aplicaciones. Aquí te presento algunos de los tipos más comunes.
Funciones lineales
Las funciones lineales son aquellas que se representan en una gráfica como una línea recta. La forma general de una función lineal es f(x) = mx + b, donde m es la pendiente y b es la intersección con el eje y. Piensa en esto como una pista de patinaje: es suave y constante. Por ejemplo, si tienes una función que describe el costo de las entradas a un concierto, podría ser lineal si el precio es constante.
Funciones cuadráticas
Las funciones cuadráticas, por otro lado, tienen la forma f(x) = ax² + bx + c. Su gráfica forma una parábola, que puede abrirse hacia arriba o hacia abajo. Imagina lanzar una pelota al aire; el camino que sigue es similar a la forma de una parábola. Este tipo de función es útil en situaciones donde hay un cambio en la tasa de crecimiento, como el área de un círculo que aumenta al variar su radio.
Funciones exponenciales
Las funciones exponenciales son aquellas en las que la variable está en el exponente, como f(x) = a * b^x. Estas funciones crecen o decrecen a un ritmo que se acelera con el tiempo. Un buen ejemplo es el crecimiento de una población o el interés compuesto en finanzas. ¡Es como si estuvieras viendo crecer una planta a una velocidad sorprendente!
La importancia de las funciones en la vida cotidiana
Ahora que hemos cubierto los conceptos básicos, es interesante ver cómo las funciones influyen en nuestra vida diaria. Desde las finanzas hasta la ingeniería, las funciones están en el corazón de muchas disciplinas. Pero, ¿cómo se manifiestan realmente en el día a día?
Funciones en finanzas
Cuando hablamos de finanzas, las funciones son fundamentales. Por ejemplo, el interés compuesto se puede modelar con una función exponencial. Cada vez que ahorras dinero, el banco no solo te paga intereses sobre tu capital inicial, sino también sobre los intereses acumulados. ¡Es como una bola de nieve que crece a medida que rueda colina abajo!
Funciones en tecnología
Las funciones también son cruciales en el desarrollo de software. Cada vez que utilizas una aplicación, hay funciones detrás que determinan cómo se comporta. Por ejemplo, cuando subes una foto a una red social, hay funciones que manejan el tamaño de la imagen, la compresión y la carga en el servidor. Todo esto se puede representar mediante funciones matemáticas que optimizan el rendimiento y la experiencia del usuario.
Resolviendo problemas con funciones
Las funciones no solo son una teoría; son herramientas poderosas para resolver problemas. Aquí te muestro cómo puedes aplicar el concepto de funciones para resolver situaciones prácticas.
Ejemplo de un problema cotidiano
Imagina que quieres saber cuánto dinero tendrás en tu cuenta de ahorros después de un año si depositas una cantidad inicial y el banco te ofrece un interés del 5% anual. Puedes usar la función de interés compuesto para calcularlo: A = P(1 + r/n)^(nt), donde A es el monto total, P es el capital inicial, r es la tasa de interés, n es el número de veces que se capitaliza el interés al año y t es el número de años. ¡Así de simple!
Funciones en la educación
En el ámbito educativo, las funciones son esenciales para entender conceptos más complejos en matemáticas y ciencias. Por ejemplo, al estudiar física, muchas fórmulas se basan en funciones que describen el movimiento, la energía y la fuerza. Si comprendes cómo funcionan las funciones, estarás mejor preparado para enfrentar desafíos académicos.
En resumen, las funciones son un concepto fundamental en matemáticas y tienen un impacto significativo en muchos aspectos de nuestra vida. Desde su definición básica hasta sus aplicaciones prácticas, entender las funciones te brinda herramientas valiosas para resolver problemas y tomar decisiones informadas. Así que la próxima vez que te encuentres con una función, recuerda: es más que solo números; es una forma de entender el mundo que te rodea.
¿Puedo tener una función que no sea matemática?
¡Por supuesto! Las funciones pueden ser vistas como relaciones o reglas en cualquier contexto, no solo en matemáticas. Por ejemplo, en programación, una función puede ser un bloque de código que realiza una tarea específica.
¿Todas las relaciones son funciones?
No. Para que una relación sea considerada una función, cada entrada debe tener una única salida. Si una entrada tiene múltiples salidas, entonces no es una función.
¿Cómo puedo practicar funciones en la vida diaria?
Una buena forma de practicar es observar situaciones cotidianas y pensar en las funciones que las describen. Por ejemplo, al calcular gastos, el tiempo que tardas en llegar a un lugar o incluso el crecimiento de tus plantas puede ser modelado por funciones.
¿Las funciones siempre son lineales?
No. Existen muchas formas de funciones, como las cuadráticas y las exponenciales. Cada tipo tiene su propia forma de representar la relación entre las entradas y salidas.
¿Por qué es importante entender las funciones?
Comprender las funciones es esencial porque te ayuda a resolver problemas, hacer predicciones y tomar decisiones informadas en diversas áreas, desde la ciencia hasta la economía.