¡Hola! Si alguna vez te has preguntado sobre el misterio de las funciones seno y coseno, has llegado al lugar indicado. Estas dos funciones son fundamentales en el mundo de las matemáticas, especialmente en la trigonometría. Pero, ¿realmente sabes qué las diferencia? No te preocupes, aquí vamos a desglosar todo esto de una manera sencilla, casi como si estuviéramos charlando en una cafetería. ¿Listo? ¡Vamos allá!
¿Qué es el Seno?
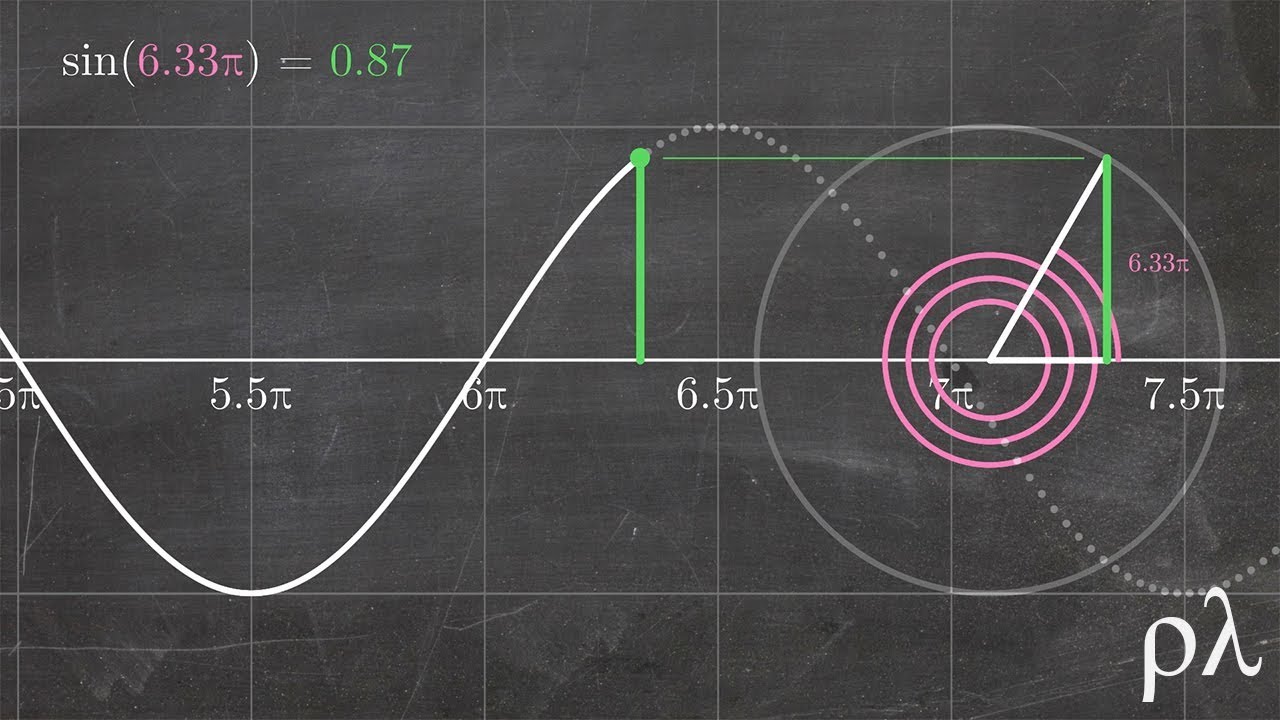
Comencemos por el seno. Imagina que estás en un círculo unitario, que es un círculo con un radio de 1. Ahora, si trazas un ángulo desde el eje horizontal, el seno de ese ángulo es simplemente la longitud de la línea vertical que se extiende desde el punto donde el ángulo toca el círculo hasta el eje horizontal. En otras palabras, el seno te dice cuán alto sube esa línea. Si el ángulo es de 0 grados, el seno es 0. Pero si el ángulo es de 90 grados, el seno alcanza su punto máximo, que es 1. ¡Es como escalar una montaña! Cuanto más alto subes, mayor es el valor del seno.
¿Qué es el Coseno?
Ahora, pasemos al coseno. Siguiendo con nuestra analogía del círculo unitario, el coseno de un ángulo es la longitud de la línea horizontal que va desde el punto donde el ángulo toca el círculo hasta el eje vertical. Así que, si piensas en el coseno, estás hablando de cuán lejos te alejas del eje vertical. En este caso, cuando el ángulo es 0 grados, el coseno es 1, y a medida que aumentas el ángulo, el coseno comienza a disminuir, llegando a 0 cuando el ángulo es de 90 grados. ¡Es como correr hacia la derecha! Cuanto más te alejas del eje vertical, menor es el valor del coseno.
La Relación entre Seno y Coseno
Ahora que tenemos una idea clara de qué es cada uno, hablemos de cómo se relacionan. Ambas funciones están interconectadas y, de hecho, hay una relación matemática muy interesante entre ellas: la identidad pitagórica. Esta identidad dice que para cualquier ángulo θ, se cumple que:
sin²(θ) + cos²(θ) = 1
Esto significa que si conoces el valor de seno de un ángulo, puedes encontrar el coseno, y viceversa. Es como tener un rompecabezas donde una pieza te ayuda a encajar la otra. Si el seno es 0.6, puedes usar esta identidad para encontrar que el coseno es aproximadamente 0.8. ¡Es un juego de matemáticas muy entretenido!
Ejemplos Clave de Seno y Coseno
Ejemplo 1: Ángulo de 30 Grados
Imagina que tienes un ángulo de 30 grados. ¿Sabías que el seno de 30 grados es 0.5 y el coseno es aproximadamente 0.866? Esto significa que, si dibujas ese ángulo en el círculo unitario, la línea vertical subirá hasta la mitad (0.5) y la línea horizontal se extenderá un poco más allá de la mitad (0.866). ¡Es como tener un pequeño triángulo donde puedes visualizar cómo se comportan estas funciones!
Ejemplo 2: Ángulo de 45 Grados
Ahora, pasemos a un ángulo de 45 grados. Aquí, tanto el seno como el coseno son iguales: ambos son aproximadamente 0.707. Esto es bastante interesante porque significa que el triángulo es isósceles. La altura y la base son iguales. ¿Te imaginas un triángulo perfectamente equilibrado? ¡Eso es lo que el seno y el coseno de 45 grados representan!
Ejemplo 3: Ángulo de 60 Grados
Finalmente, veamos un ángulo de 60 grados. En este caso, el seno es aproximadamente 0.866 y el coseno es 0.5. Aquí, la línea vertical sube bastante alto, mientras que la línea horizontal es más corta. Es como si estuvieras escalando una montaña empinada; subes rápido pero no te alejas tanto del eje vertical.
Aplicaciones Prácticas de Seno y Coseno
Ahora que hemos cubierto lo básico, hablemos de por qué esto es importante. Las funciones seno y coseno tienen aplicaciones en el mundo real. Por ejemplo, en la física, se utilizan para modelar ondas, como el sonido y la luz. También son esenciales en la ingeniería para calcular fuerzas y movimientos. ¿Alguna vez has escuchado sobre la oscilación de un péndulo? ¡Esa es una aplicación directa de estas funciones!
¿Por qué son Importantes en la Vida Cotidiana?
Las funciones seno y coseno no son solo para matemáticos o ingenieros. Imagina que estás diseñando una montaña rusa. Necesitas saber cómo se moverán los carros a medida que suben y bajan. Aquí es donde entran en juego el seno y el coseno. También, si alguna vez has usado un GPS, esos cálculos de posición se basan en trigonometría, que utiliza estas funciones. ¡Así que, en cierto sentido, el seno y el coseno están en todas partes!
¿El seno y el coseno son funciones periódicas?
¡Sí! Ambas funciones son periódicas, lo que significa que se repiten en intervalos regulares. La periodicidad del seno y el coseno es de 360 grados o 2π radianes. Esto es lo que hace que sean tan útiles en muchas aplicaciones.
¿Puedo usar seno y coseno en triángulos no rectángulos?
En realidad, las funciones seno y coseno son más útiles en triángulos rectángulos, pero puedes usar la ley de senos y la ley de cosenos para trabajar con triángulos no rectángulos. ¡Es como tener herramientas versátiles en tu caja de herramientas matemáticas!
¿Cuál es la relación entre el seno y el coseno en diferentes cuadrantes?
Excelente pregunta. En el primer cuadrante, ambos son positivos. En el segundo, el seno es positivo y el coseno es negativo. En el tercer cuadrante, ambos son negativos, y en el cuarto, el seno es negativo mientras que el coseno es positivo. ¡Es como una montaña rusa de signos!
¿Cómo puedo recordar los valores del seno y coseno para ángulos comunes?
Una buena forma de recordar estos valores es crear una pequeña tabla o utilizar el famoso mnemotécnico de «SOH-CAH-TOA». Esto te ayudará a recordar que el seno es la opuesta sobre la hipotenusa, el coseno es la adyacente sobre la hipotenusa, y la tangente es la opuesta sobre la adyacente. ¡Es un truco fácil que puede salvarte en un examen!
¿Existen otras funciones trigonométricas relacionadas?
¡Por supuesto! Además del seno y coseno, también tienes la tangente, la cosecante, la secante y la cotangente. Cada una tiene su propia relación con el seno y el coseno, y juntas forman un hermoso entramado de funciones que puedes explorar.
Así que ahí lo tienes, una guía sencilla y amigable sobre las diferencias entre seno y coseno. Espero que ahora tengas una mejor comprensión de estas funciones y cómo se aplican en el mundo real. ¡No dudes en seguir explorando y haciendo preguntas!